Transience and Recurrence of Markov Chain

An application with Symmetric Random Walk

In my previous article, I’ve been introducing Markov processes, providing the intuition behind and implementation with Python. In this article, I’m going to dwell a bit more on some properties of Markov chain and, in particular, to the so-called Recurrence of a specific Markov chain, called Symmetric Random Walk.

Let’s first briefly recap what we are talking about. A Markov chain can be defined as a stochastic process Y in which the value at each point at time t depends only on the value at time t-1. It means that the probability for our stochastic process to have state x at time t, given all its past states, is equal to the probability of having state x at time t, given only its state at t-1.

We can graphically represent our chain with a graph, where the circles are states, the arrows represent the accessibility (together with the probability of transition) between states. Let’s, for example, consider the following:

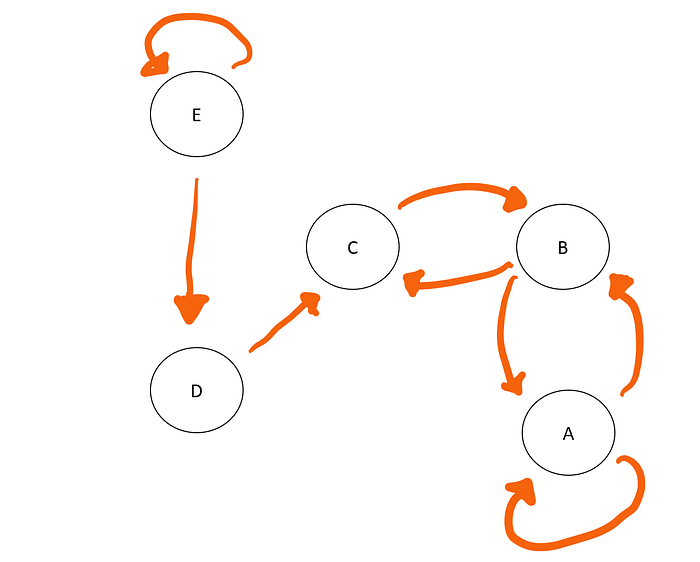
Looking at this graph, we can start talking about the two main properties of a chain, which are Recurrence and Transience.